Unit Circle Trigonometry Learning Objective(s) Understand unit circle, reference angle, terminal side, standard position Find the exact trigonometric function values for angles that measure 30°, 45°, and 60° using the unit circle Find the exact trigonometric function values of any angle whose reference angle measures 30°, 45°, or 60°About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsThe Unit Circle Ck 12 Foundation For more information and source, see on this link https//flexbooksck12org/cbook/ck12precalculusconcepts/section/51

The Unit Circle At A Glance
Unit circle quadrant 1 2 3 4
Unit circle quadrant 1 2 3 4-Start studying Unit Circle Quadrant 2 Learn vocabulary, terms, and more with flashcards, games, and other study toolsStart studying UNIT CIRCLE QUADRANT 3 Learn vocabulary, terms, and more with flashcards, games, and other study tools Search Create Log in Sign up Log in Sign up 25 terms cbmiller17 UNIT CIRCLE QUADRANT 3 STUDY PLAY 180 coordinates (1,0) 180 radians π sin of 180 0 cos of 1801 tan of 180 0 210 coordinates ( √3/2, 1/2
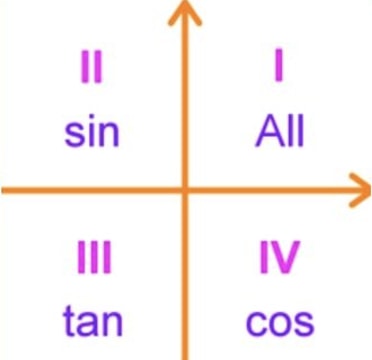



What Is All Students Take Calculus In Trig Studypug
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsQuestion 6162 Find the quadrant (1, 2, 3, or 4) containing the points on the unit circle satisfying the given conditions csc(t) > 0 tan(t) > 0 Answer by fcabanski(1390) (Show Source)1 150 o 2 1 3 7 4 S 4 2 3 S II Determine the quadrant in which the terminal side of the Solve the following problems using your Unit Circle 1) sin(90 ) D 2) cos 4 3) 5 sin 4 4) cos 135D 5) 5 tan 4 6)tan(180 )D 7 The given point P is located on the Unit Circle State the quadrant and find the angle , also sin , cos and tan 1
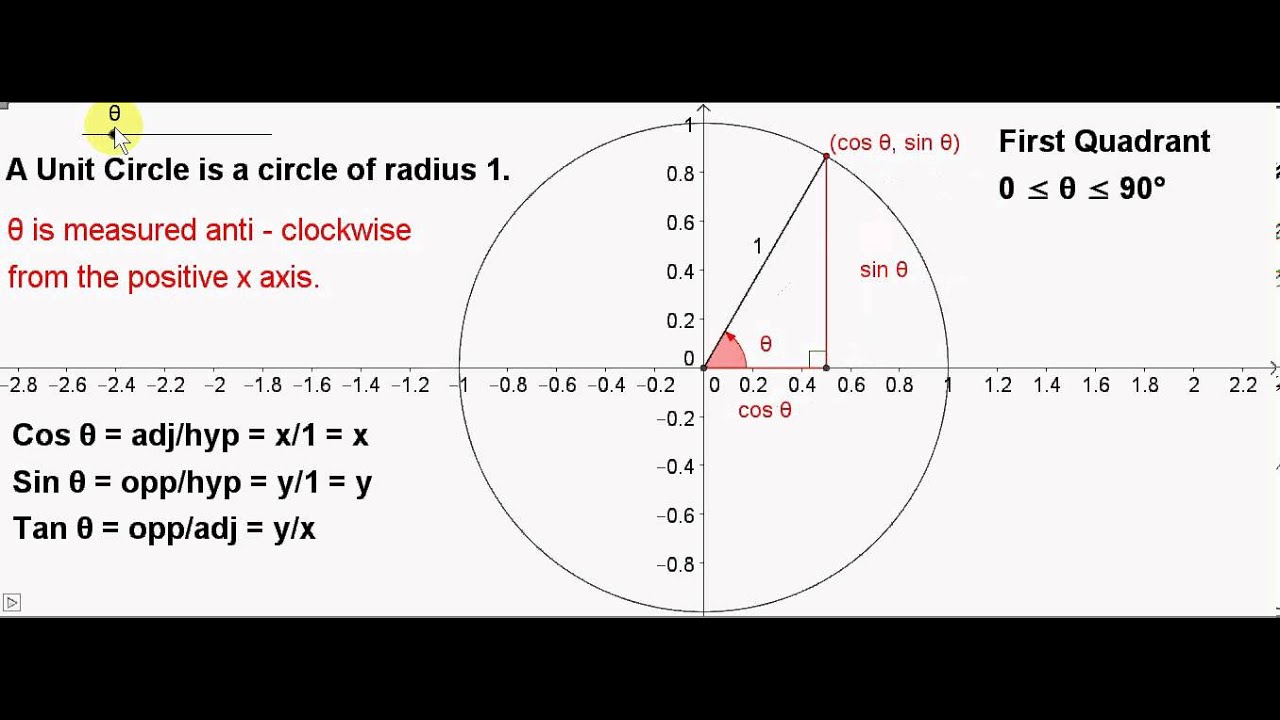
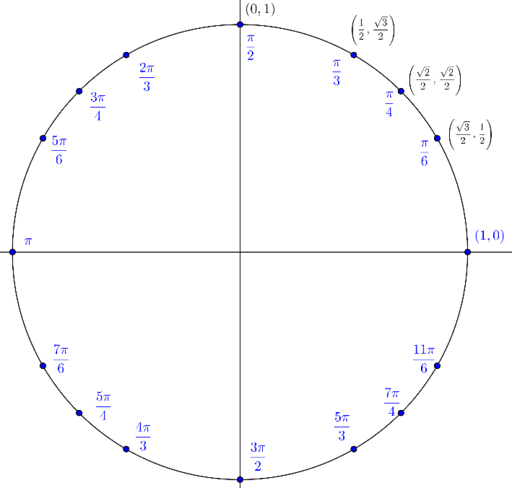
66Provided by the Academic Center for Excellence 6 The Unit Circle Updated October 19 Practice Problems Find the exact value of the problems below using either the standard unit circle or the triangle method 1) Sin 4𝜋 3 2) Cos 11𝜋 6 3) Tan 𝜋 3 4) Cos −2𝜋 3 (Hint Instead of rotating counterclockwise around the circle, goIn this video I explain the first quadrant of the unit circleThe unit circle below shows the values of the cosine and sine functions (coordinates in blue, with the xcoordinate being the cosine and the ycoordinate is the sine) for the special angles 0, π/6 (30 °), π/4 (45 °), π/3 (60 °), π/2 (90 °), 2π/3 (1 °), 5π/4 (135 °)
Unit circle help If the point P(14/15,y) is on the unit circle in quadrant IV, then y= I don't understand how to get to the answer and I seem to get 0359 asPlay this game to review Precalculus sin π/4 74 Unit Circle Quadrant 1 DRAFT 11th 12th grade 117 times Mathematics % average accuracy 17 days ago abaumer 0 Save Edit Edit 74 Unit Circle Quadrant 1 DRAFT 17 days ago by abaumer Played 117 times 0 11thUnit Circle Trigonometry Drawing Angles in Standard Position Examples The following angles are drawn in standard position 1 θ=40D 2 160θ= D 3 θ=−3D Exercises Sketch each of the following angles in standard position (Do not use a protractor;



Unit Circle Angles In The First Quadrant Youtube



Key Angles In The Unit Circle Geogebra
View Unit Circle (1)pdf from MATH Algebra 2 at Richard Montgomery High Unit Circle and Reference Angles 1 3 − , 2 2 2π 3 2 2 − 2 , 2 3π 4 1 3 , 2 23 On an interval of latex\left0,2\pi \right)/latex, can the sine and cosine values of a radian measure ever be equal?Correct answers 3 question Angle 0 corresponds to a point (x, y) on the unit circle in quadrant 1 Which quadrant does 0pi lie in?



1



Unit Circle Calculator Inch Calculator
1) −5° 2)−155° 3)25° 4)335° 6 Which angle does not terminate in Quadrant IV when drawn on a unit circle in standard position?Pythagoras Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides x 2 y 2 = 1 2 But 1 2 is just 1, so x 2 y 2 = 1 equation of the unit circle Also, since x=cos and y=sin, we get (cos(θ)) 2 (sin(θ)) 2 = 1 a useful "identity" Important Angles 30°, 45° and 60° You should try to remember sin1) Start from point 0, which is located on the xaxis between Quadrant One & Quadrant 4 2) Begin counting the given units (either degrees, or radians) in a counterclockwise manner 3) Once the reference point is determined, draw a line to the nearest xaxis to get the reference triangle
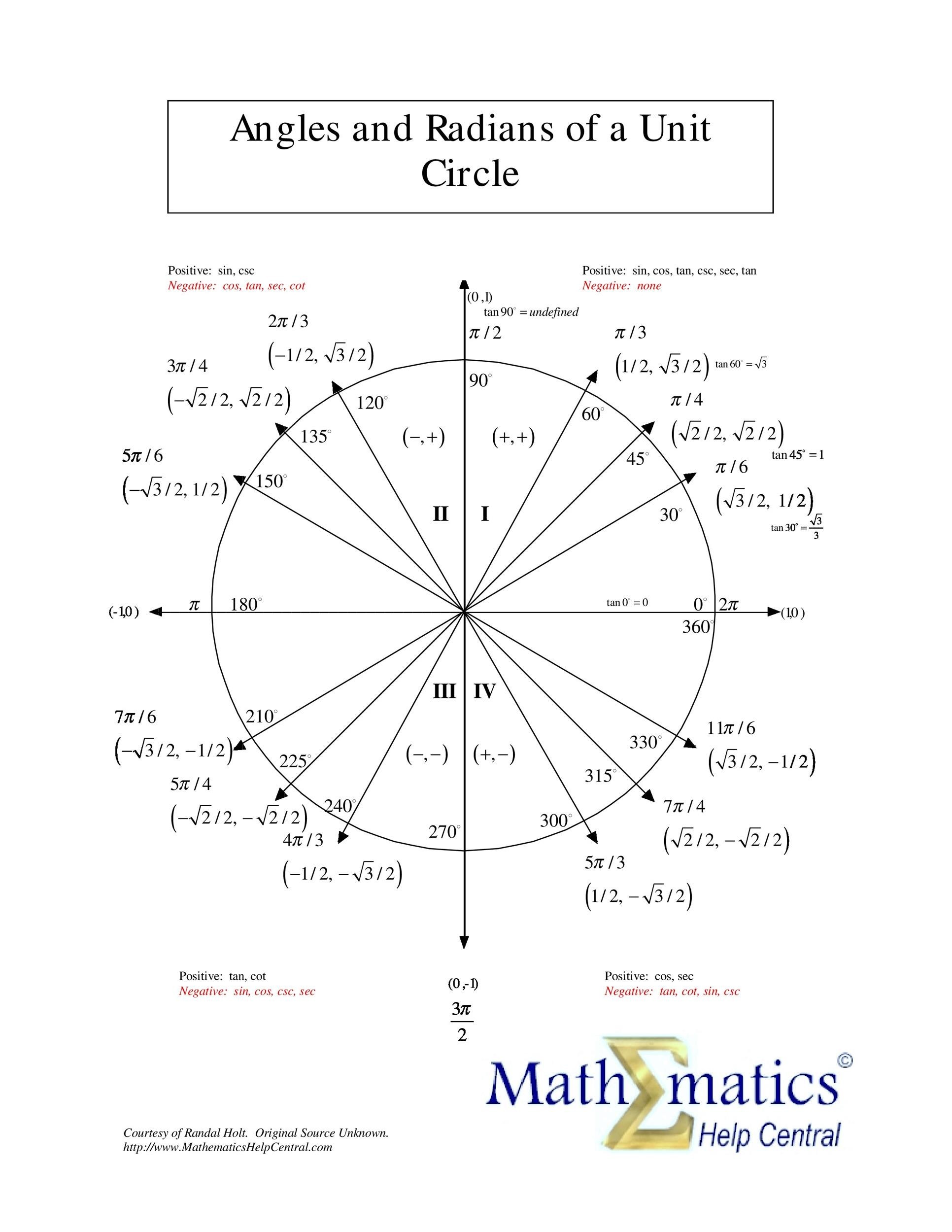



42 Printable Unit Circle Charts Diagrams Sin Cos Tan Cot Etc




5 1 The Unit Circle The Unit Circle
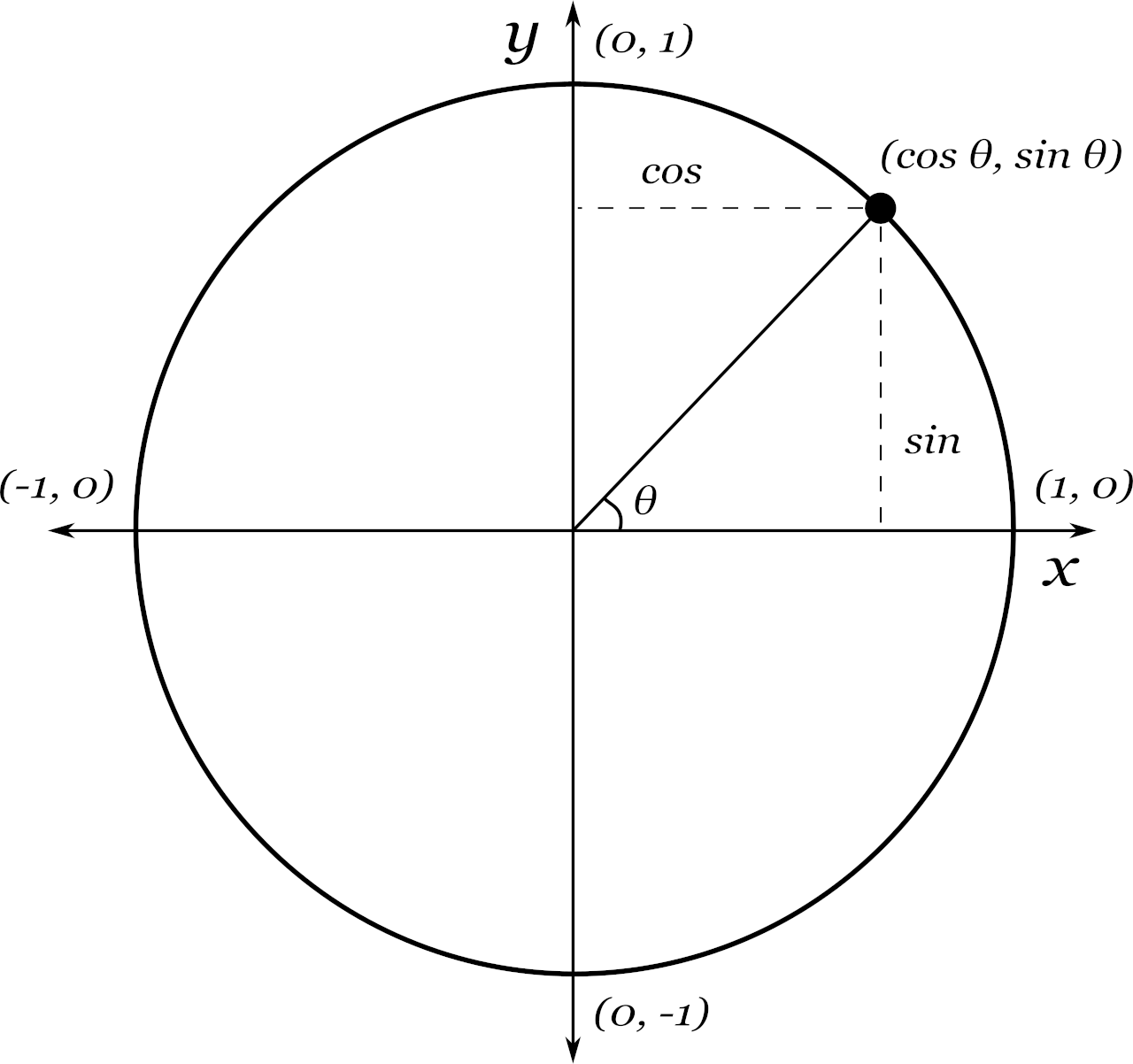
Recall that the equation for the unit circle is x2 y2 = 1 x 2 y 2 = 1 Because x= cost x = c o s t and y = sint, y = s i n t, we can substitute for x x and y y to get cos2tsin2t= 1 c o s 2 t s i n 2 t = 1 This equation, cos2tsin2t =1, c o s 2 t s i n 2 t = 1, is known as the Pythagorean IdentityThe unit circle chart shows the position of the points along the unit circle that are formed by dividing the circle into eight and twelve parts The coordinates of each point can be solved for using the one of the two corresponding special triangles Figure 1 Unit Circle Chart π (pi)4 What would you estimate the cosine of latex\pi /latex
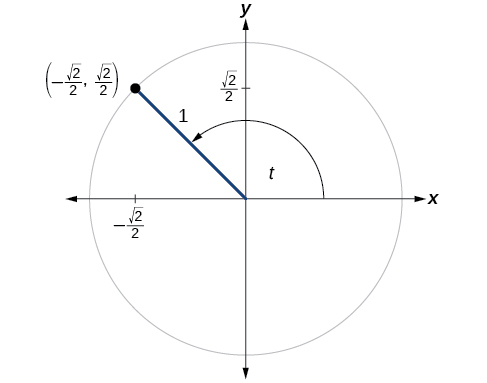



Unit Circle Algebra And Trigonometry




3 Ways To Memorize The Unit Circle Wikihow
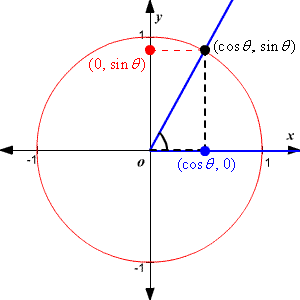
1) −300° 2)−50° 3)280° 4)1030° 7 The terminal side of an angle measuring 4π 5 radians lies in Quadrant 1) I 2) II 3) III 4) IV 8 An angle that measures 5π 6 radians is drawn in standard position InTypically, we take r = 1 That is called the unit circle, as we shall see The trigonometric functions in fact depend only on the angle θ and it is for that reason we say that they are functions of θ Example 1 A straight line inserted at the origin terminates at the point (3, 2) as it sweeps out an angle θ in standard positionEvaluate sine and cosine values using a calculator To define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in Figure 2 The angle (in radians) that t t intercepts forms an arc of length s s Using the formula s =rt s = r t, and knowing that r =1 r = 1, we see that for a
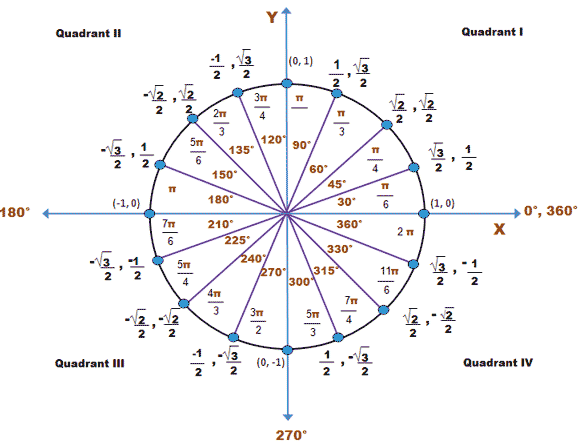



Trigonometric Functions Of Any Angle Trigonometry Socratic
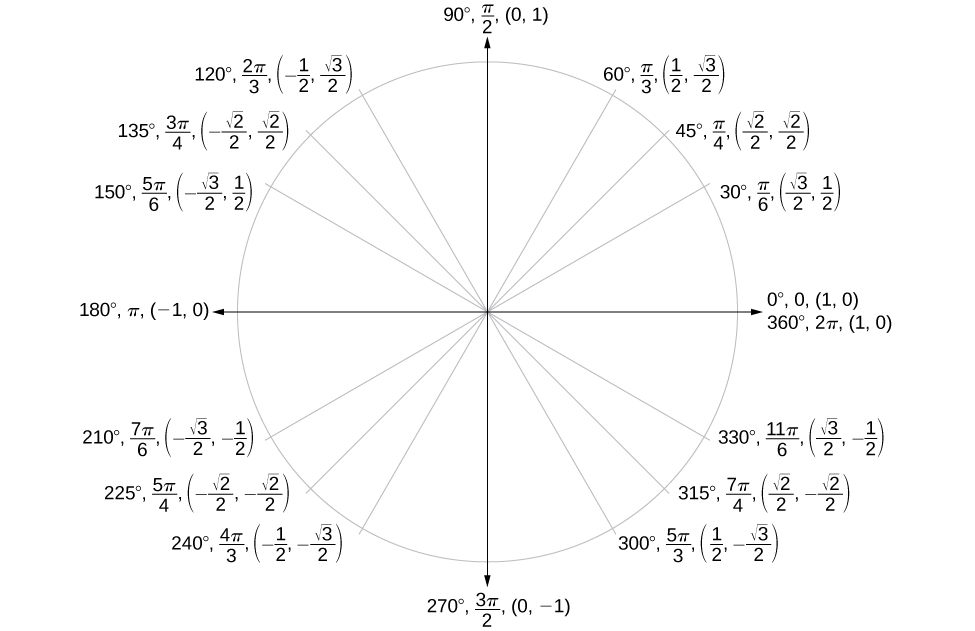



2 1 Unit Circle Sine And Cosine Functions Mathematics Libretexts
Live modes Start a live quiz Classic Students progress at their own pace and you see a leaderboard and live resultsRemainder when 2 power 256 is divided by 17 Remainder when 17 power 23 is divided by 16 Sum of all three digit numbers divisible by 6 Sum of all three digit numbers divisible by 7 Sum of all three digit numbers divisible by 8 Sum of all three digit numbers formed using 1, 3, 4 Sum of all three four digit numbers formed with non zero digits1 csc 11 4 S o 2 cot 30 3 sec 2S 4 Find the exact values of sin T, cos , and tan if the terminal side of in standard position contains the given point P(1, 8) 5 Suppose is an angle in standard position whose terminal side lies in the given quadrant Find the exact values of the remaining five trig functions of for sin = 4 5



1



4 Unit Circle Trig Functions Identities
Section 42 Homework Exercises 1 Describe the unit circle 2 What do the x and ycoordinates of the points on the unit circle represent?Of the circle A full revolution of a circle ( 360∘ 360 ∘) equals 2π radians 2 π r a d i a n s This means that 1 radian = 180∘ π 1 radian = 180 ∘ π The formula used to convert between radians and degrees is angle in degrees = angle in radians⋅ 180∘ π angle in degrees = angle in radians ⋅ 180 ∘ π The radian measure ofJust draw a brief sketch) 1 1θ= D 2 45θ=− D 3 130θ=− D 4 θ=270D θ=−90D 6
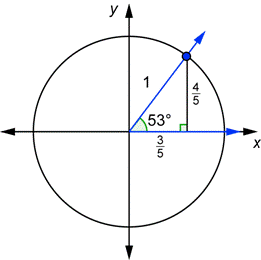



Unit Circle Trigonometry



The Point P X 1 3 Lies On The Unit Circle And Is In Quadrant 4 What Is The Sketch Of A Unit Circle Showing The Point P And The Principal Standard Position Angle
The point P is on the unit circle If the ycoordinate of P is 4/5 and P is in quadrant III , then x = ?Cartesian Coordinates Using Cartesian Coordinates we mark a point on a graph by how far along and how far up it is The point (12,5) is 12 units along, and 5 units up Four Quadrants When we include negative values, the x and y axes divide the space up into 4 pieces Quadrants I, II, III and IV (They are numbered in a counterclockwise direction) In Quadrant I both x and y are positive,Learn unit circle quadrant 1 with free interactive flashcards Choose from 500 different sets of unit circle quadrant 1 flashcards on Quizlet
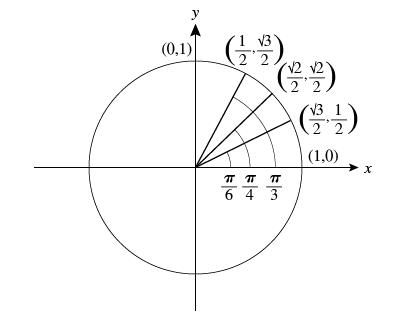



Solved The Unit Circle In Detail In Figure 4 There Are Chegg Com




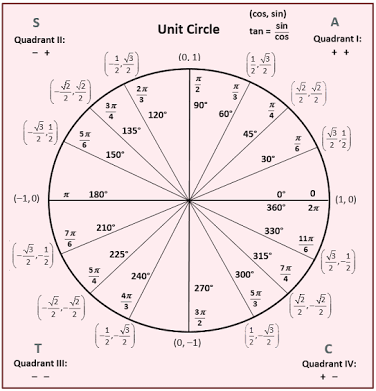
Unit Circle Chart
1) 30° 2) 60° 3) 1° 4) 150° 13 If θ is an angle in standard position and its terminal side passes through point − 1 2, 3 2 on the unit circle, then a possible value of θ is 1) 60º 2) 1º 3) 150º 4) 330º 14 In the accompanying diagram of a unit circle, the ordered pair − 3 2,− 1 2View Day 3 Using the Unit Circle revised from MATH 1112 at Kennesaw State University Math 1112 Using the Unit Circle Quadrant Name _ in Degrees in Radians 1 3 , 2 2 1 2 30o IIActivity 3 Find the xand ycoordinates for each angle in Quadrants II, III, and IV Note The equation for the Unit Circle is x2 y2 = 1 Recall When both (x, y) and (x, y) are on a graph, you have yaxis symmetry When both (x, y) and (x, y) are on a graph, you have xaxis symmetry
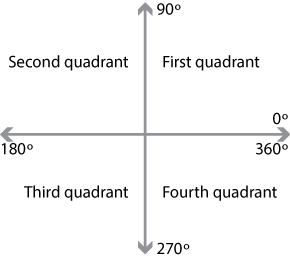



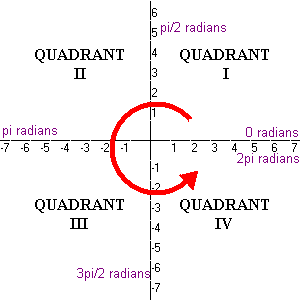
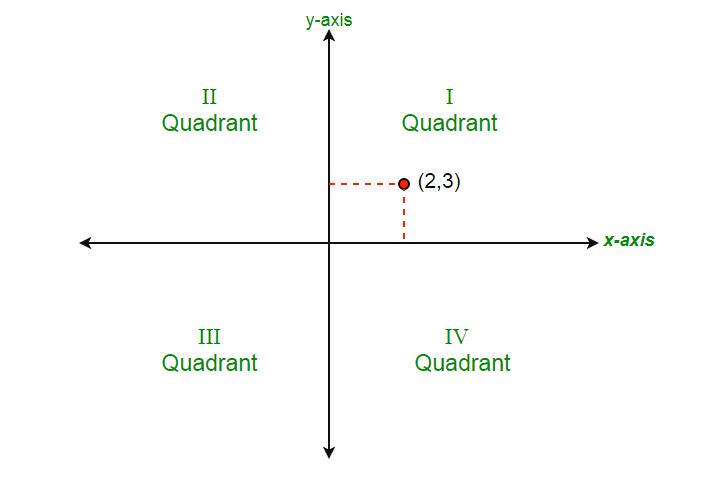
Content The Four Quadrants
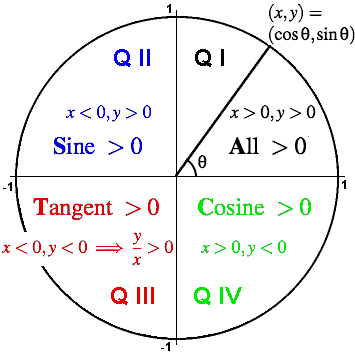



Trigonometry Facts The Amazing Unit Circle
2 1, 2 3 By drawing a the triangle inside the unit circle with a 30 degree angle and reflecting it over the line y = x, we can find the cosine and sine for 60 degrees, or 3 π, without any additional work 2 By this symmetry, we can see the coordinates of the point on the unit circle at an angle of 60 degrees will be 2 3, 2 1, giving 2 1Start studying Quadrants 14 Unit Circle Quiz Learn vocabulary, terms, and more with flashcards, games, and other study tools Adding together the 2 in the numerator and the 3 in the denominator will yield 5 Look at the angle straight across in quadrant 4 (bottom right quarter of the circle) Place this 5 in the numerator in front of π Repeat this process for the other two angles in quadrants 2 and 4
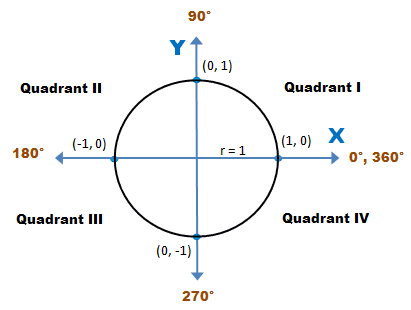



Trigonometry Snow Mountain



View Question Unit Circle
The coordinates for the point on a circle of radius at an angle of are At the radius of the unit circle, 1, serves as the hypotenuse of a degree right triangle, as shown in Angle has measure At point we draw an angle with measure of We know the angles in a triangle sum to so the measure of angle is also Now we have an equilateral triangle Because each side of the equilateralFind the Other Trig Values in Quadrant I csc (x)=4 csc(x) = 4 csc ( x) = 4 Use the definition of cosecant to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the values csc(x) = hypotenuse opposite csc ( x) = hypotenuse oppositeAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
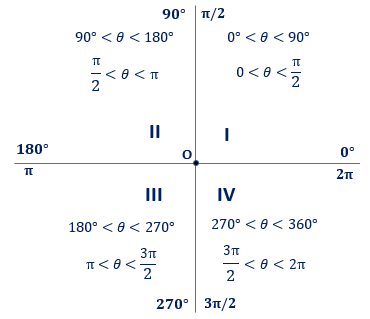



Unit Circle Javatpoint
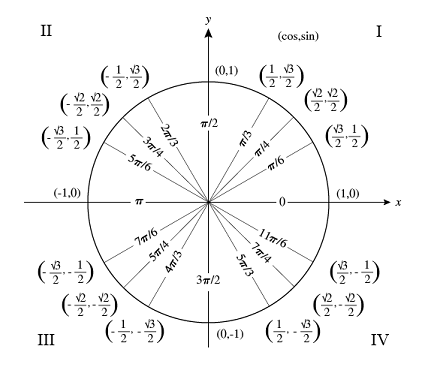



Solved The Unit Circle In Detail In Figure 4 There Are Chegg Com
Therefore In Quadrant II, cos(θ) 0, sin(θ) > 0 and tan(θ) 0 (Sine positive) For an angle in the third quadrant the point P has negative x and y coordinates Therefore In Quadrant III, cos(θ) 0, sin(θ) 0 and tan(θ) > 0 (Tangent positive) For an angle in the fourth quadrant the point P has positive x coordinate and negative y coordinateStart studying Sin, cos, tan (all 4 quadrants) LearnPreview this quiz on QuizizzWe have discussed the unit circle for the first quadrant Similarly, we can extend and find the radians for all the unit circle quadrants The numbers 1/2, 1/√2, √3/2, 0, 1 repeat along with the sign in all 4 quadrants




Solved Student Activity 3 Use Quadrant 1 From The Unit Chegg Com



Eleventh Grade Lesson Developing The Unit Circle Betterlesson
Seema Sharma $150 PDF I teach the unit circle by reminding students of and special right triangles with their ratios and connecting it to the reference angles on the unit circle in each quadrant This practice worksheet allows students to connect the 2 concepts together betterUNIT CIRCLE Quadrant 1 Only DRAFT 21 minutes ago by p_159 10th 12th grade Mathematics Played 1 times 0 likes 92% average accuracy 0 Save Edit Edit Print;A lesson to help you understand and memorize unit circle angles in quadrant 1 This is the foundation for understanding the whole unit circle!!



Year 10a Chapter 04 Introducing The Unit Circle Activity Builder By Desmos




Unit Circle
The inverse tangent function, tan−1(a) tan − 1 ( a) is sometimes called the arctangent function, and notated arctan(a) arctan ( a) Caution47 Based only on the definitions above, the inverse trigonometric functions are not actually functions at all!For example, since sin(0)= 0 sin



How Do You Determine The Quadrant In Which 6 02 Radians Lies Socratic



Tangent Function



Applying Trig Functions To Angles Of Rotation Trigonometry Socratic
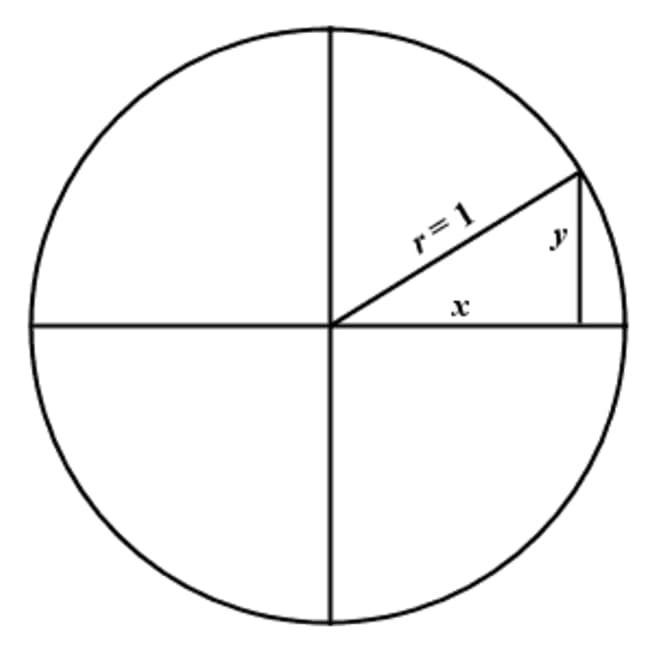



Understanding The Unit Circle Studypug



Unit Circle Angles In The Second Quadrant Youtube



Program To Determine The Quadrant Of The Cartesian Plane Geeksforgeeks



Special Angles




Unit Circle Memorizing The First Quadrant Video Lesson Transcript Study Com




The Unit Circle Exact Measurements And Symmetry Consider The




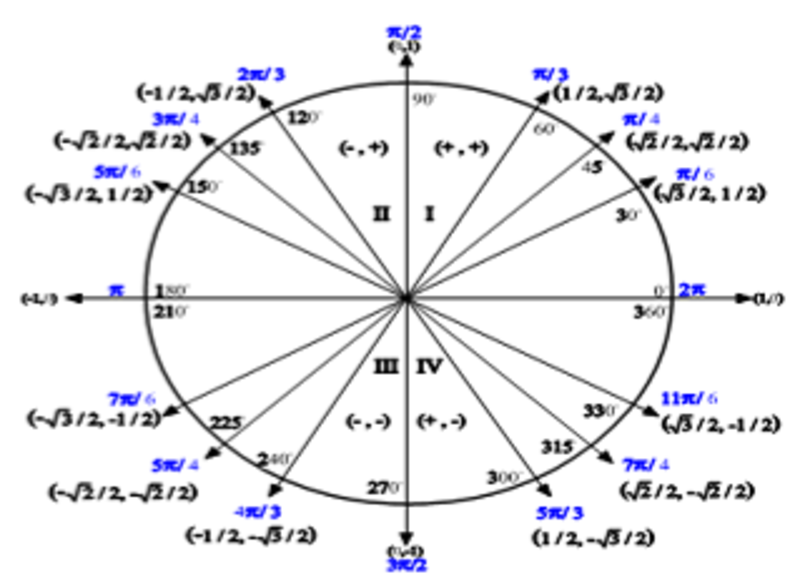
The Unit Circle Ck 12 Foundation
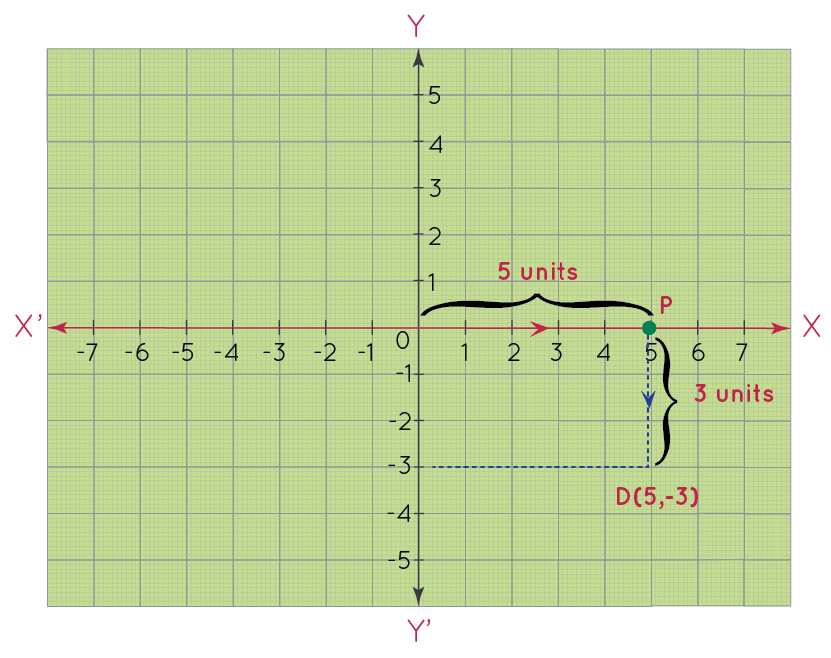



What Is Quadrant Definition Coordinate Graphs Examples Practice Questions




What Is All Students Take Calculus In Trig Studypug




Trig Unit Circle Review Article Khan Academy



1
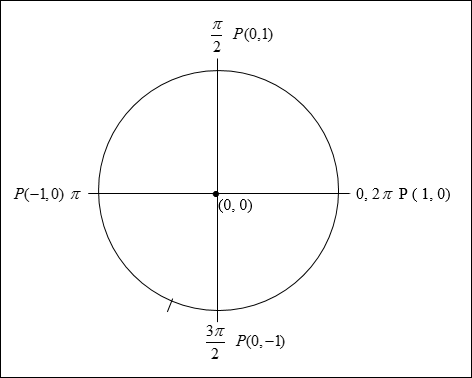



Circular Trigonometry




The Unit Circle At A Glance




The Unit Circle Ck 12 Foundation
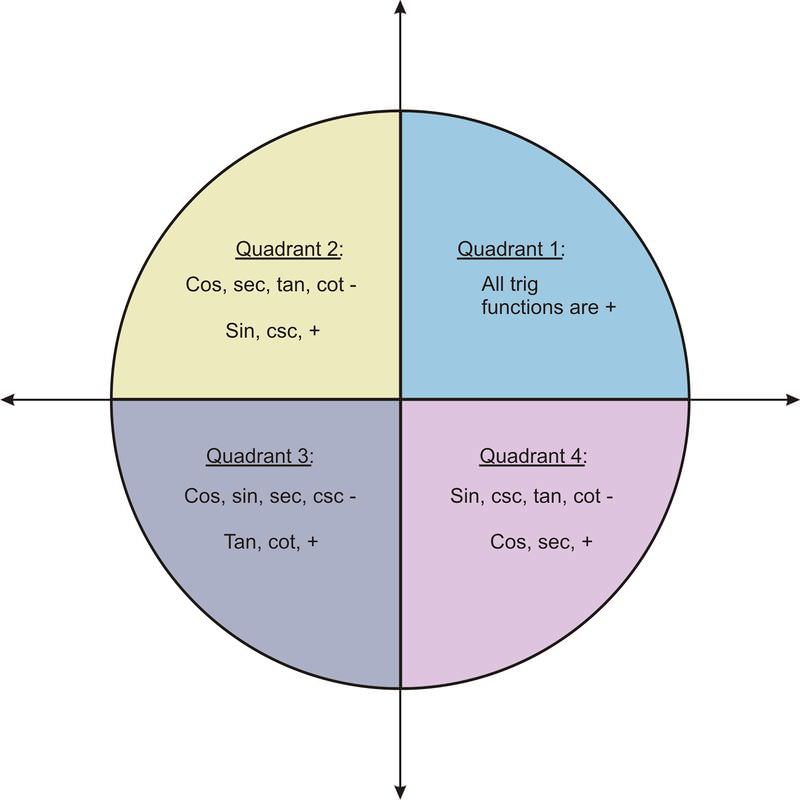



Domain Range And Signs Of Trigonometric Functions Ck 12 Foundation
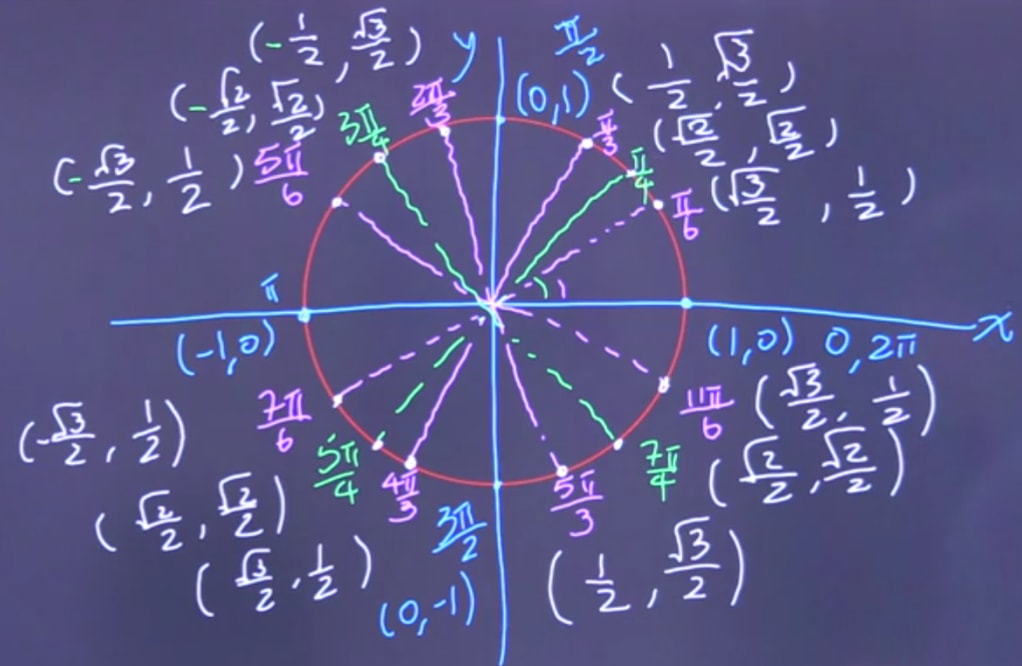



Understanding The Unit Circle Studypug
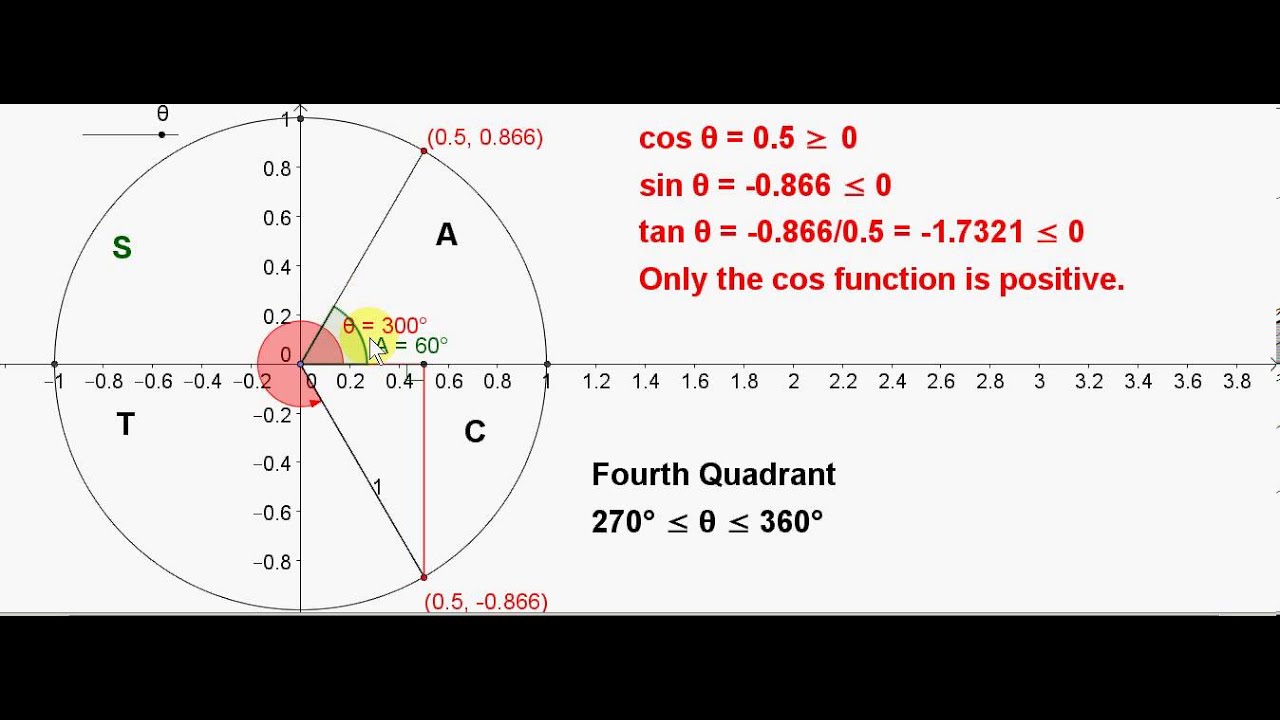



Unit Circle Angles In The Fourth Quadrant Youtube



4 Unit Circle Trig Functions Identities
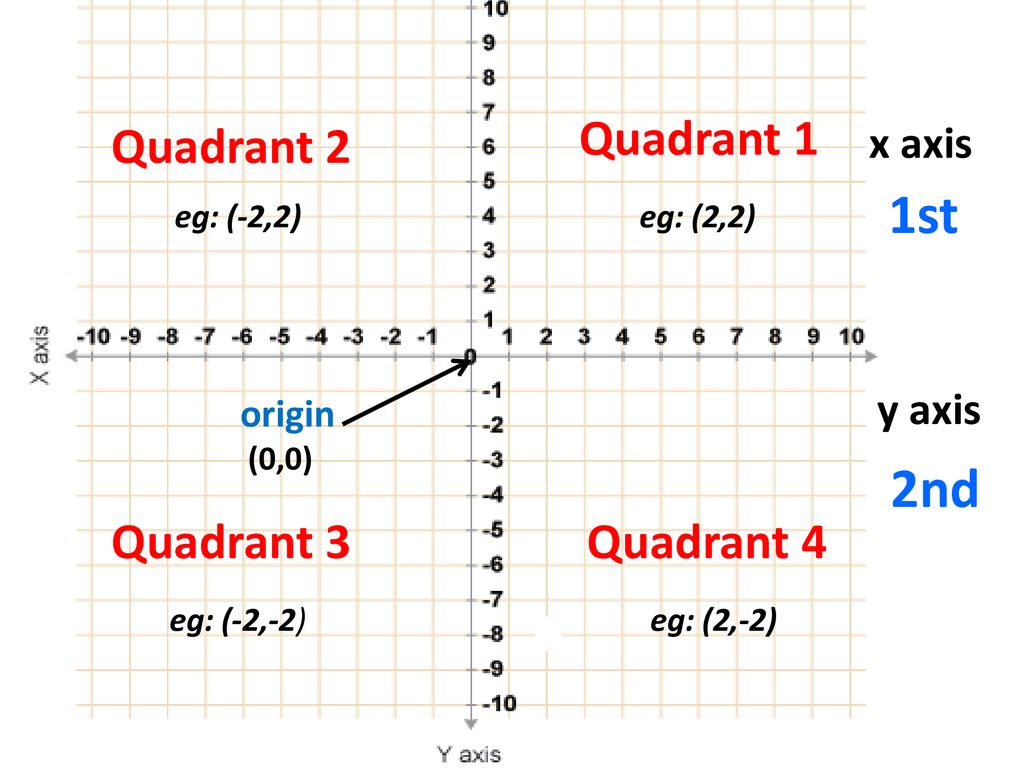



Co Ordinates In All 4 Quadrants Ppt Download
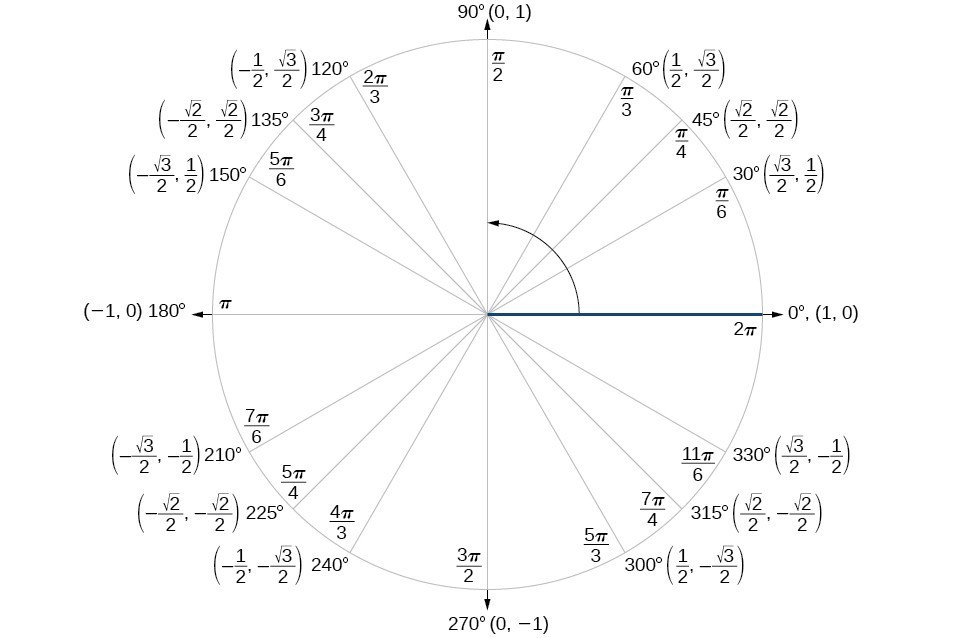



Sum And Difference Identities Precalculus Ii
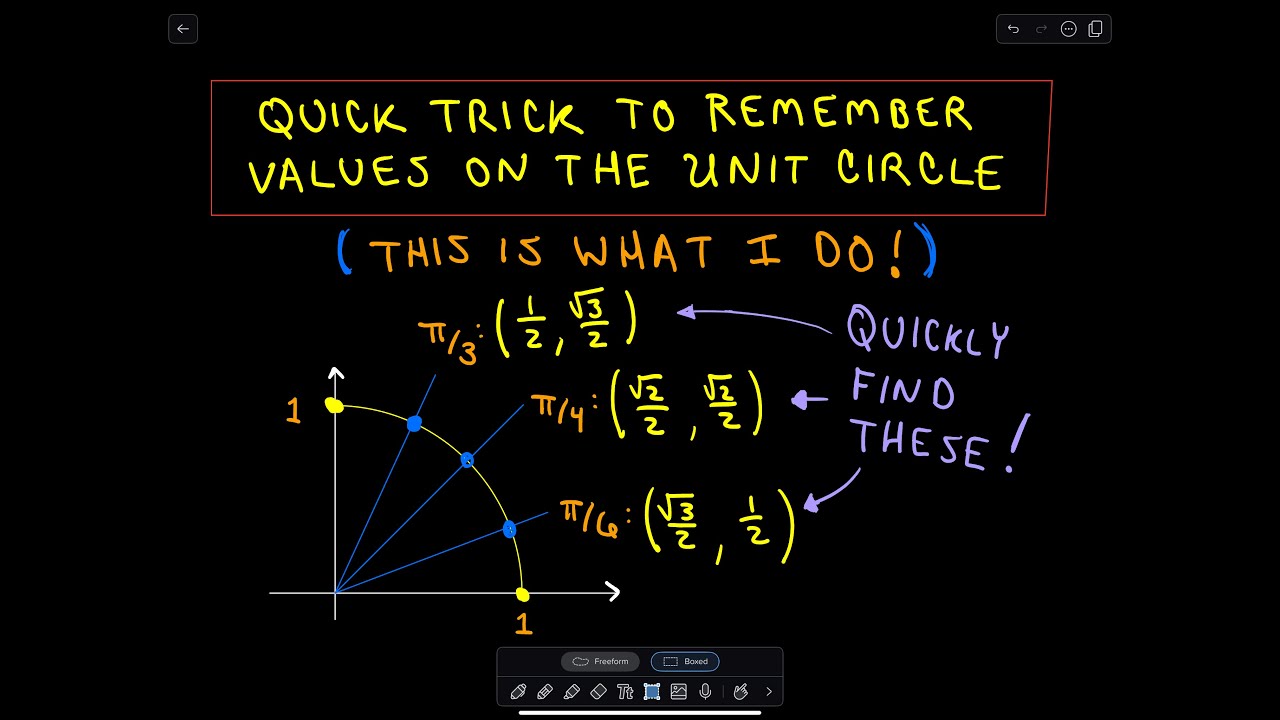



A Trick To Remember Values On The Unit Circle Youtube
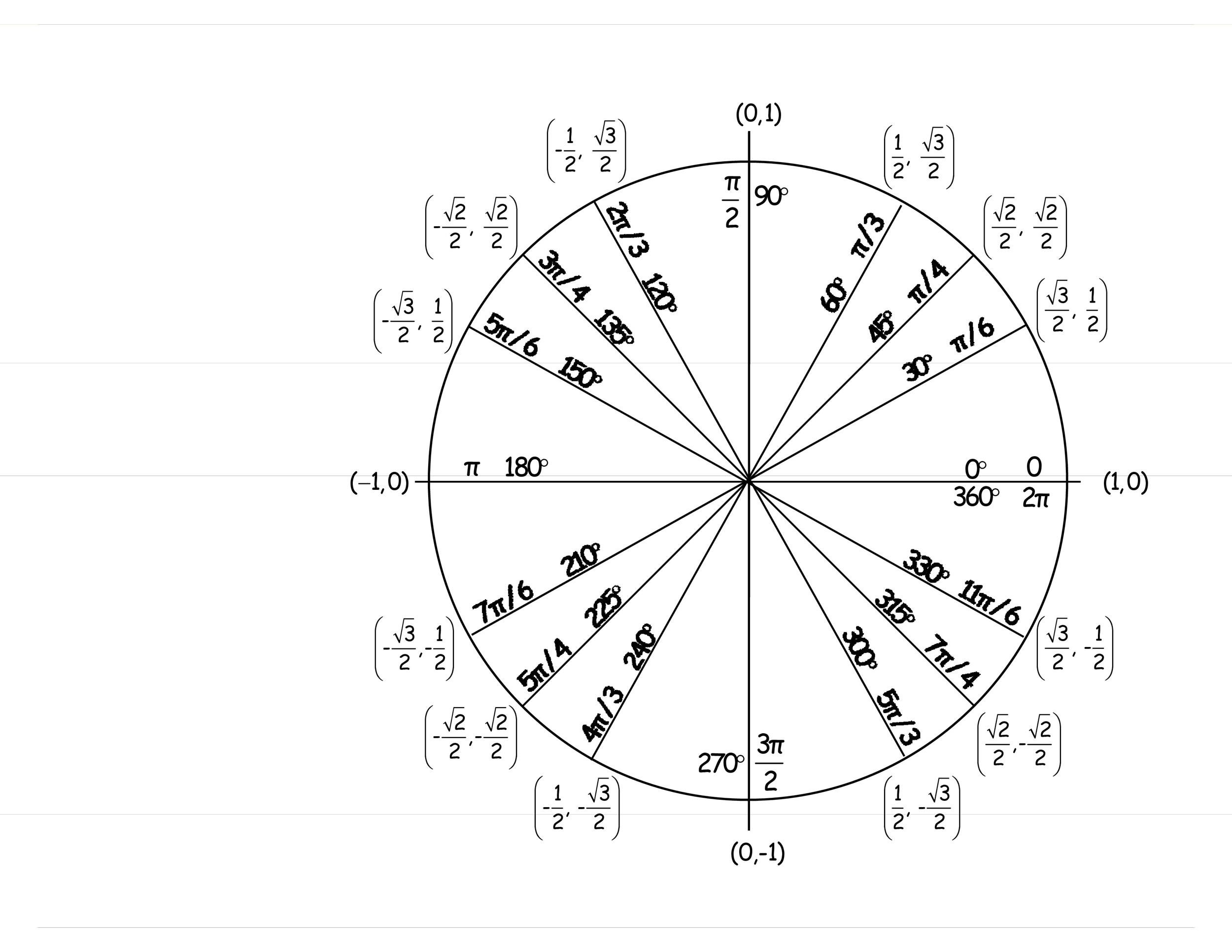



42 Printable Unit Circle Charts Diagrams Sin Cos Tan Cot Etc
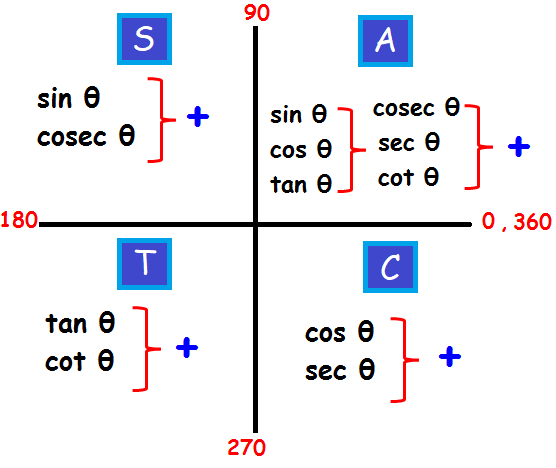



Trigonometry Quadrant Formulas



Cast Rule Mathonline
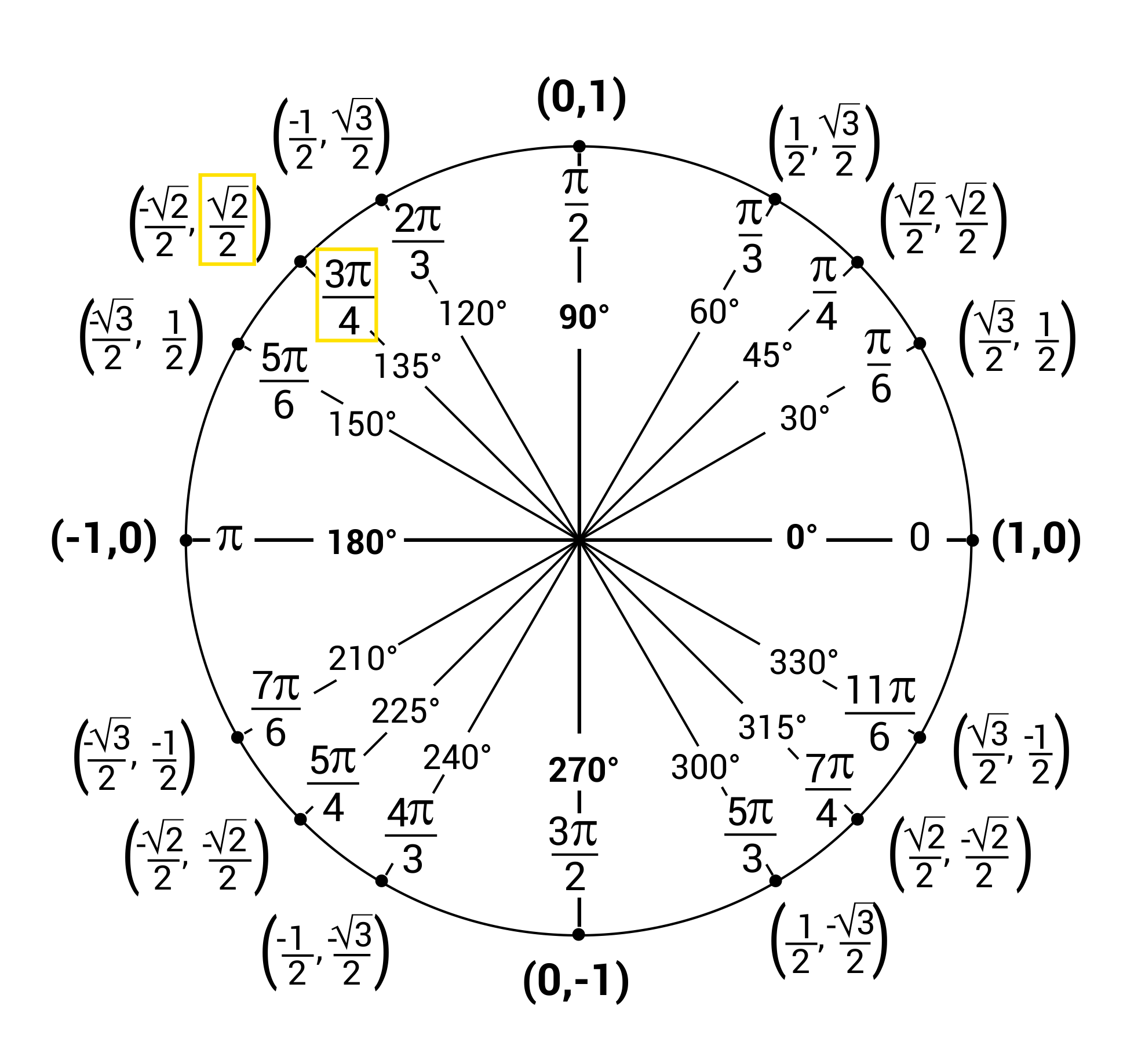



Unit Circles And Standard Position Video Practice




Astc Formula
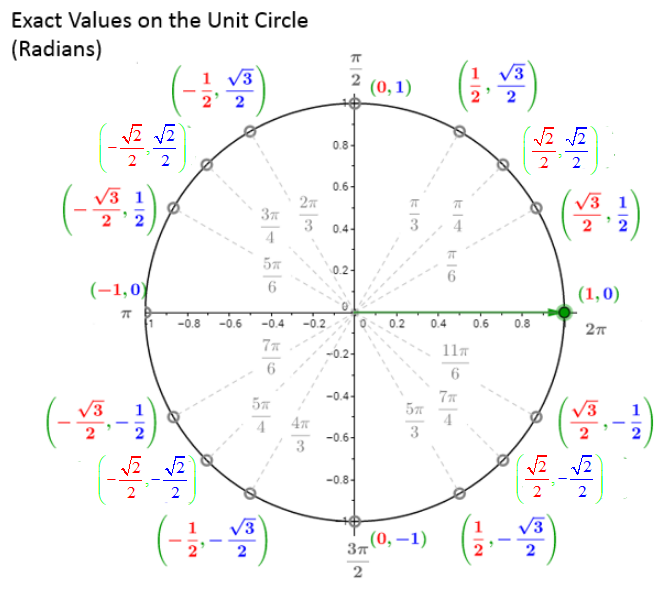



Math Tricks To Remember The Unit Circle Video Lessons Examples And Solutions
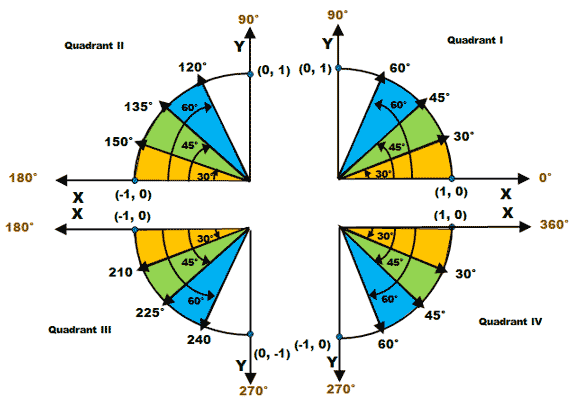



Trigonometry Snow Mountain




Sine Cosine And Tangent In Four Quadrants
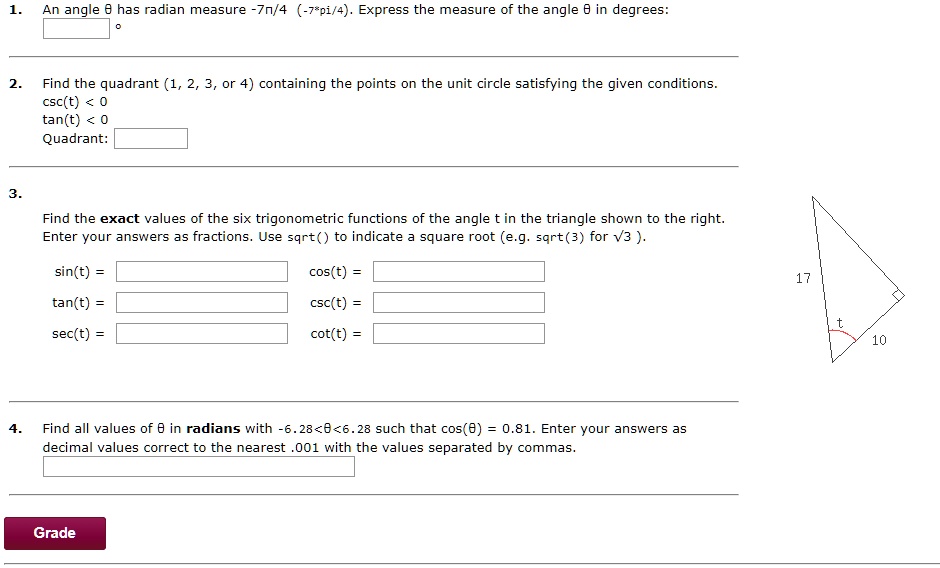



Solved An Angle Has Radian Measure 7n 4 7 01 4 Express The Measure Of The Angle In Degrees Find The Quadrant 1 2 3 Or 4 Containing The Points On The Unit Circle Satisfying The



Special Angles In The Unit Circle
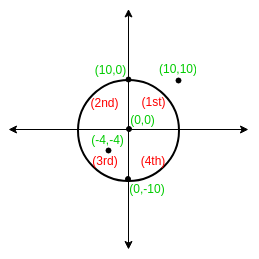



Finding Quadrant Of A Coordinate With Respect To A Circle Geeksforgeeks



1
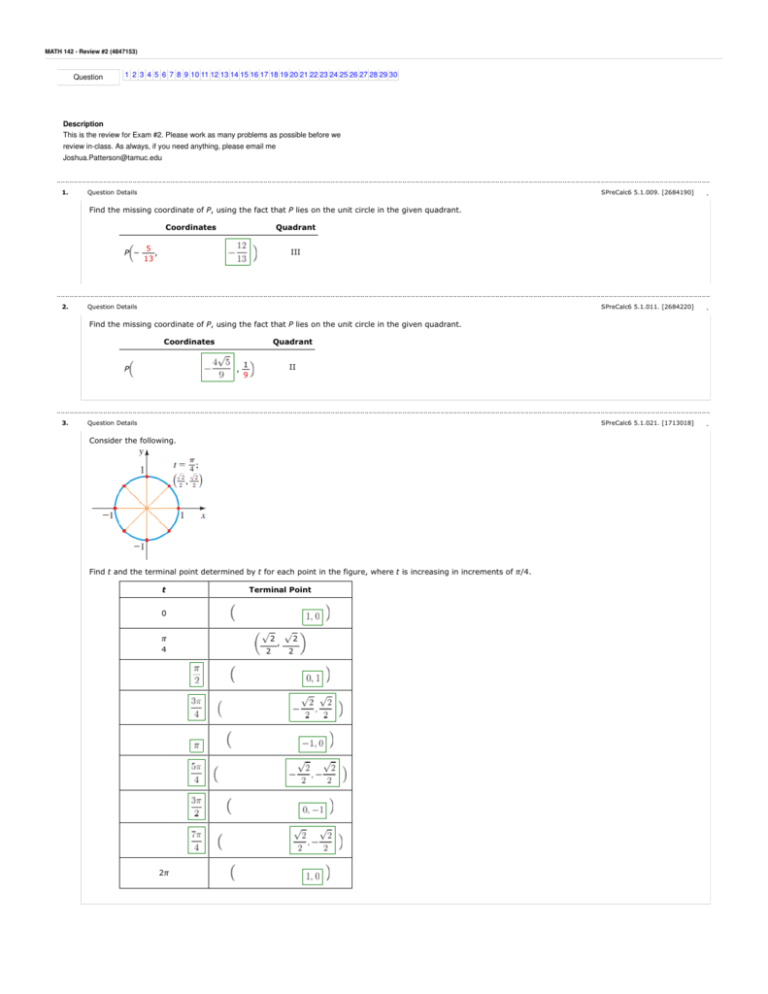



Exam 2 Review Key
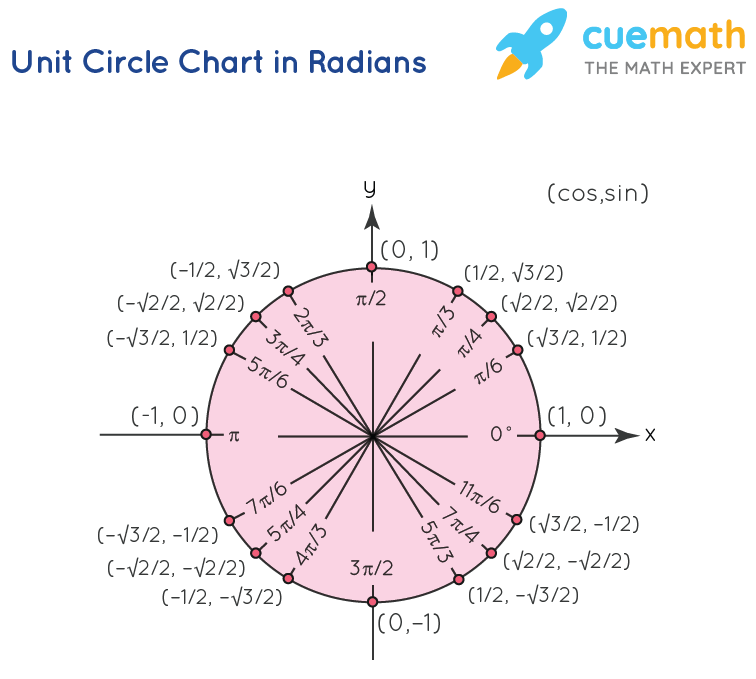



Unit Circle Equation Of A Unit Circle Unit Circle Chart
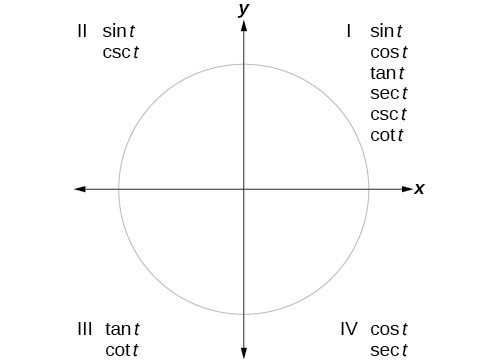



Section 4 4 Reference Angles Precalculus
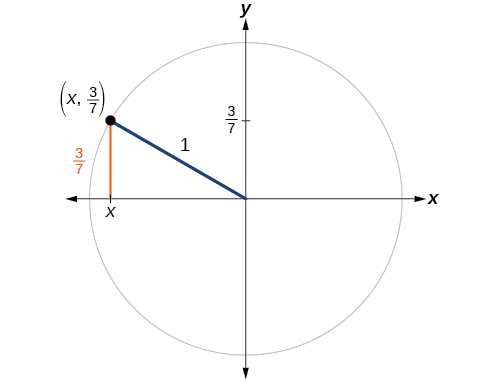



2 1 Unit Circle Sine And Cosine Functions Mathematics Libretexts
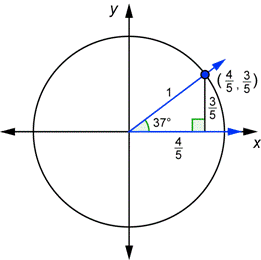



Unit Circle Trigonometry
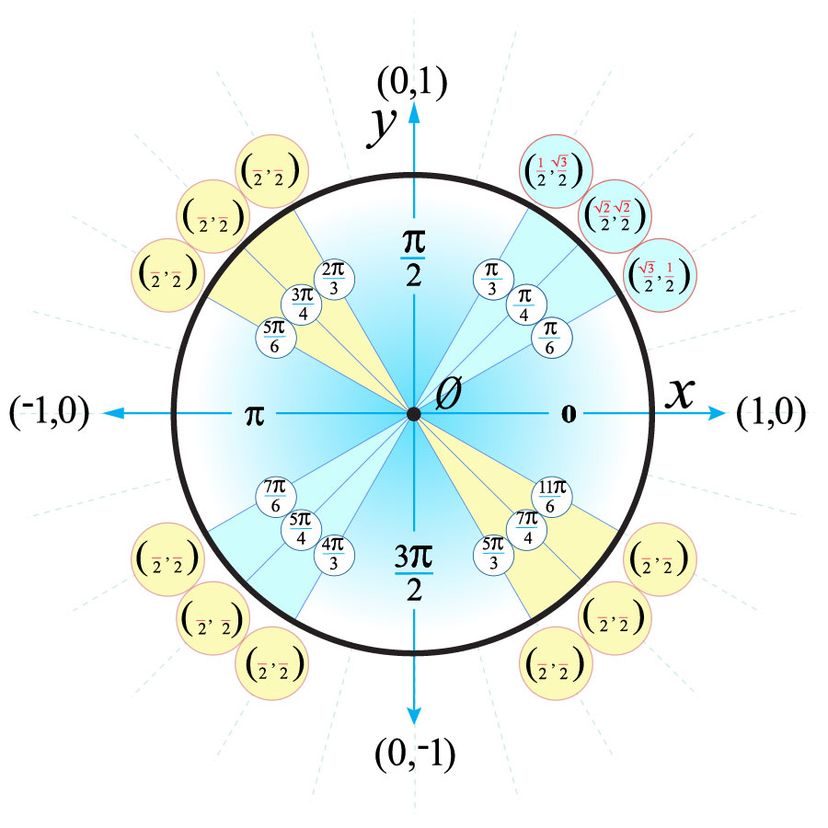



How To Use The Unit Circle In Trig Howstuffworks




Trigonometry




Unit Circle
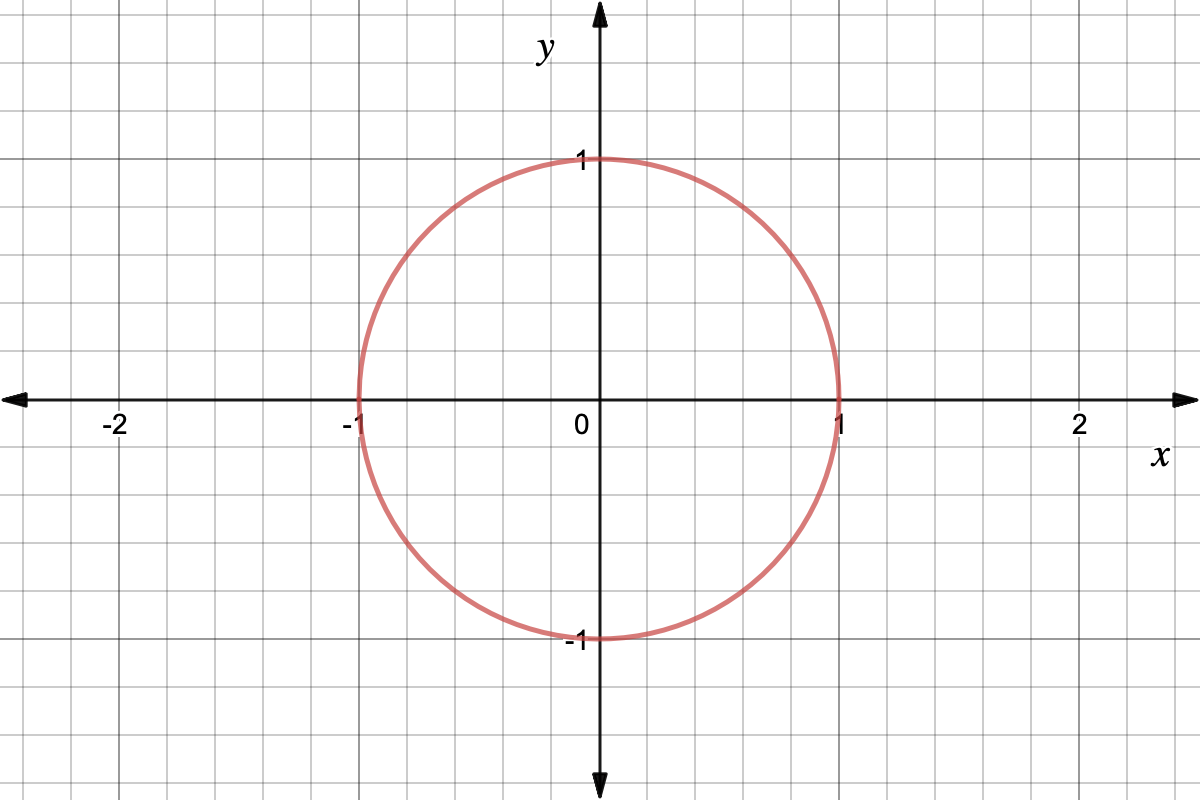



What Is The Unit Circle Expii
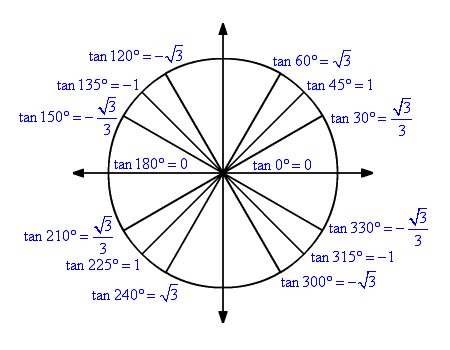



Tangent Function
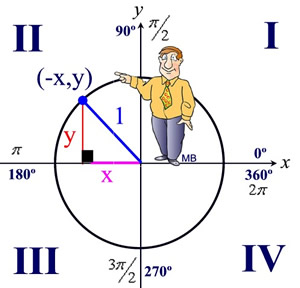



Unit Circle Mathbitsnotebook Ccss Math



Determining Values On The Unit Circle Mathonline
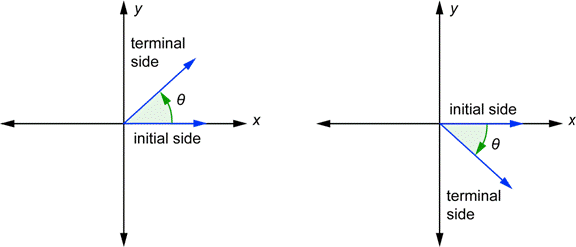



Unit Circle Trigonometry
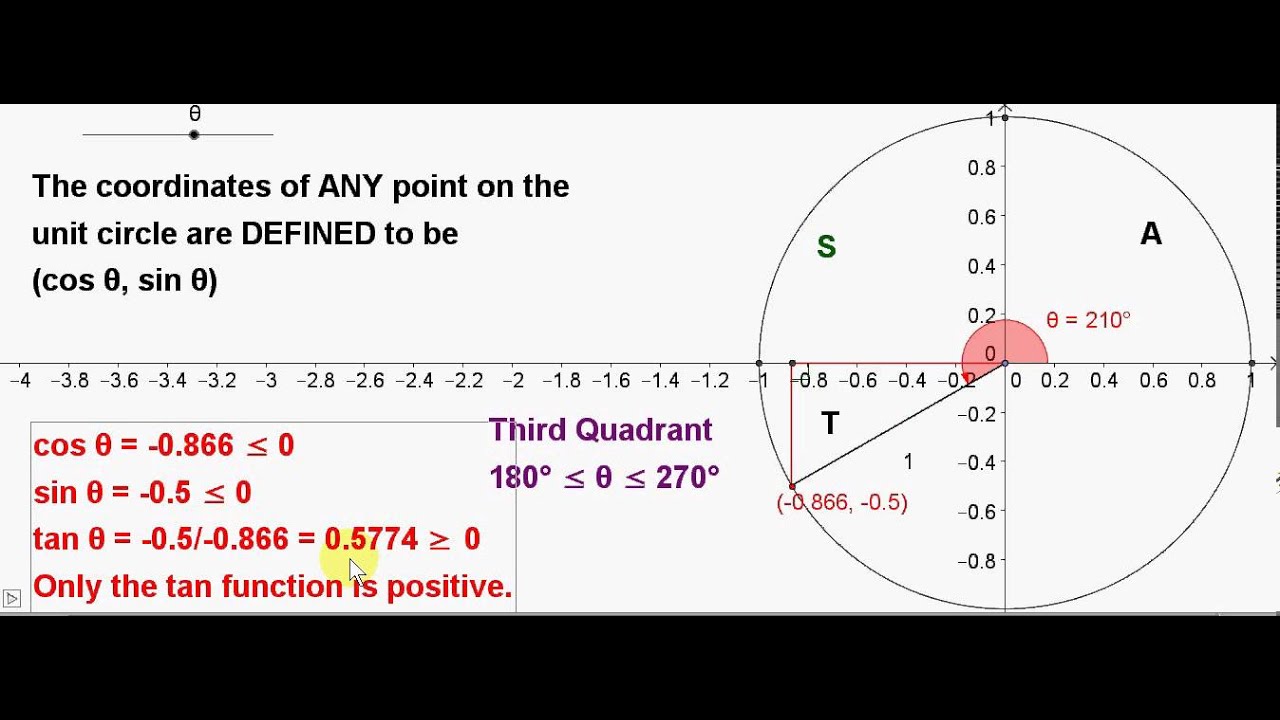



Unit Circle Angles In The Third Quadrant Youtube



4 Unit Circle Trig Functions Identities




The Unit Circle Ck 12 Foundation




Unit Circle Problem Tan Ratio In The Third Quadrant Mathematics Stack Exchange
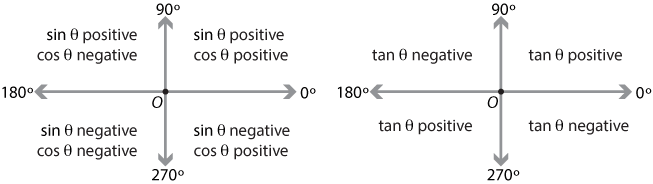



Content The Four Quadrants
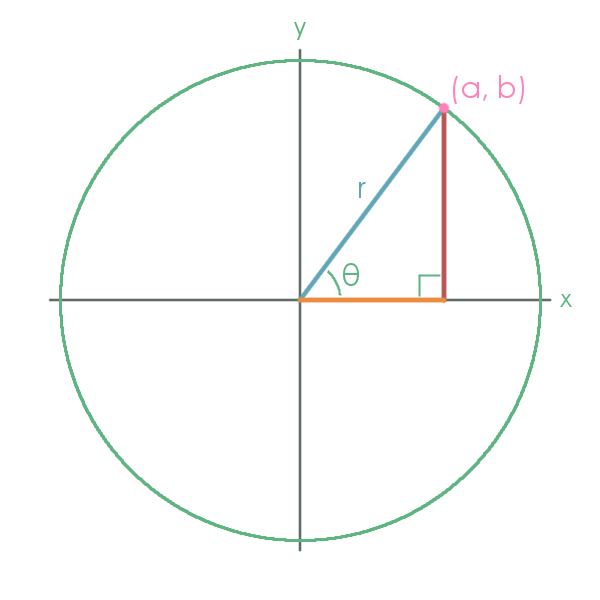



Using Unit Circle To Find Sine Or Cosine Expii



How To Use The First Quadrant Of The Unit Circle To Find The Value Of Sin 7pie 6 Quora
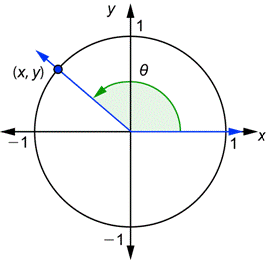



Unit Circle Trigonometry




The Unit Circle At A Glance



The Trigonometric Ratios Of Angl
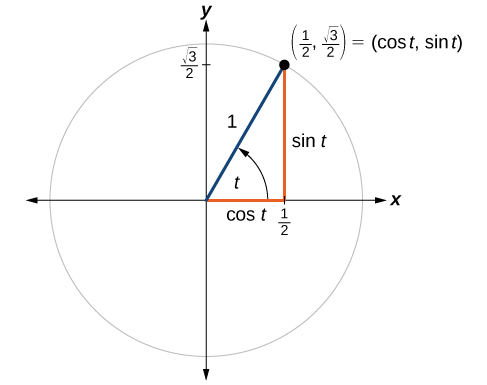



Unit Circle Algebra And Trigonometry
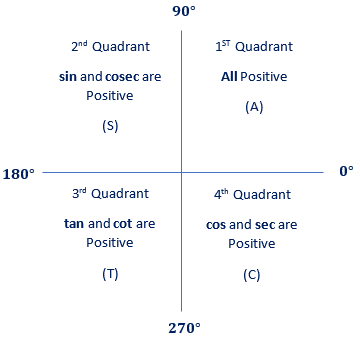



Unit Circle Javatpoint
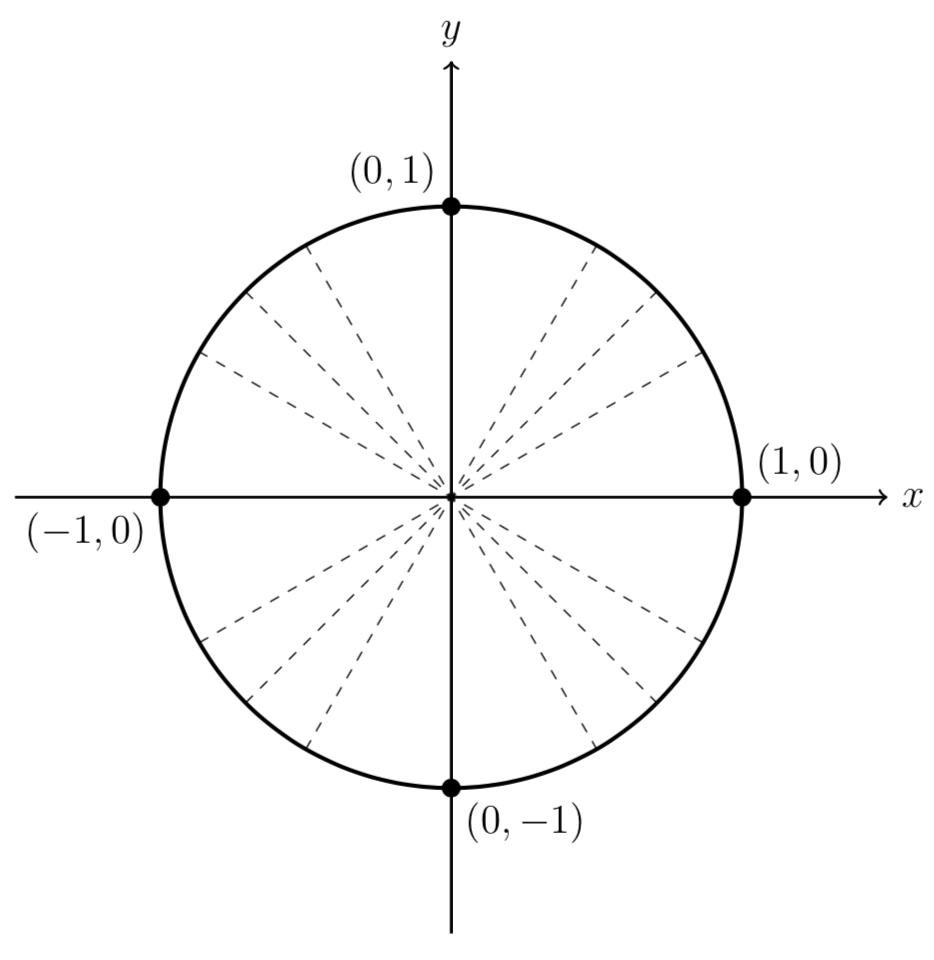



Mfg The Unit Circle




Standard Coordinates In Quadrants Ii Iii And Iv Of The Unit Circle Youtube



Exact Trig Values




Printable Unit Circle Charts Diagrams Free Sin Cos Tan Cot Etc



The Unit Circle



The Trigonometric Ratios Of Angl



Unit Circle Chart
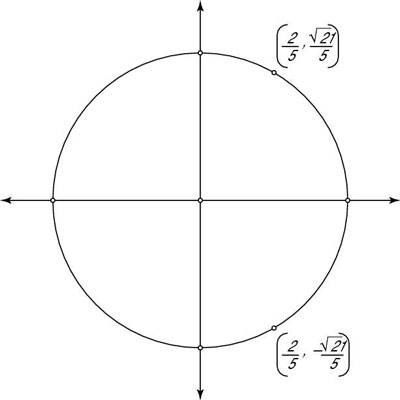



How To Find A Missing Coordinate On A Unit Circle Dummies
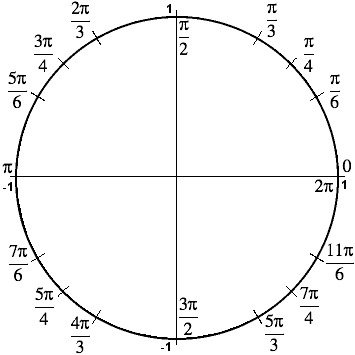



Trigonometry Facts The Amazing Unit Circle
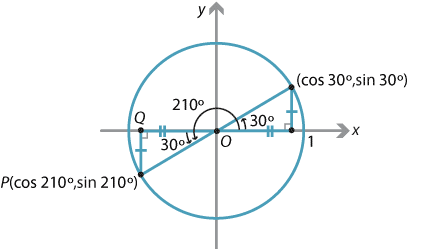



Content The Four Quadrants
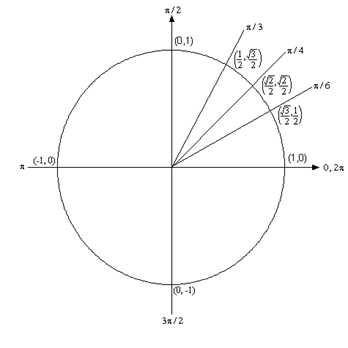



Algebra Trig Review




3 Ways To Memorize The Unit Circle Wikihow
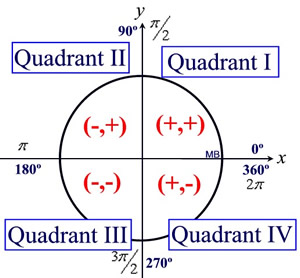



Unit Circle Mathbitsnotebook Ccss Math



Unit Circle Chart
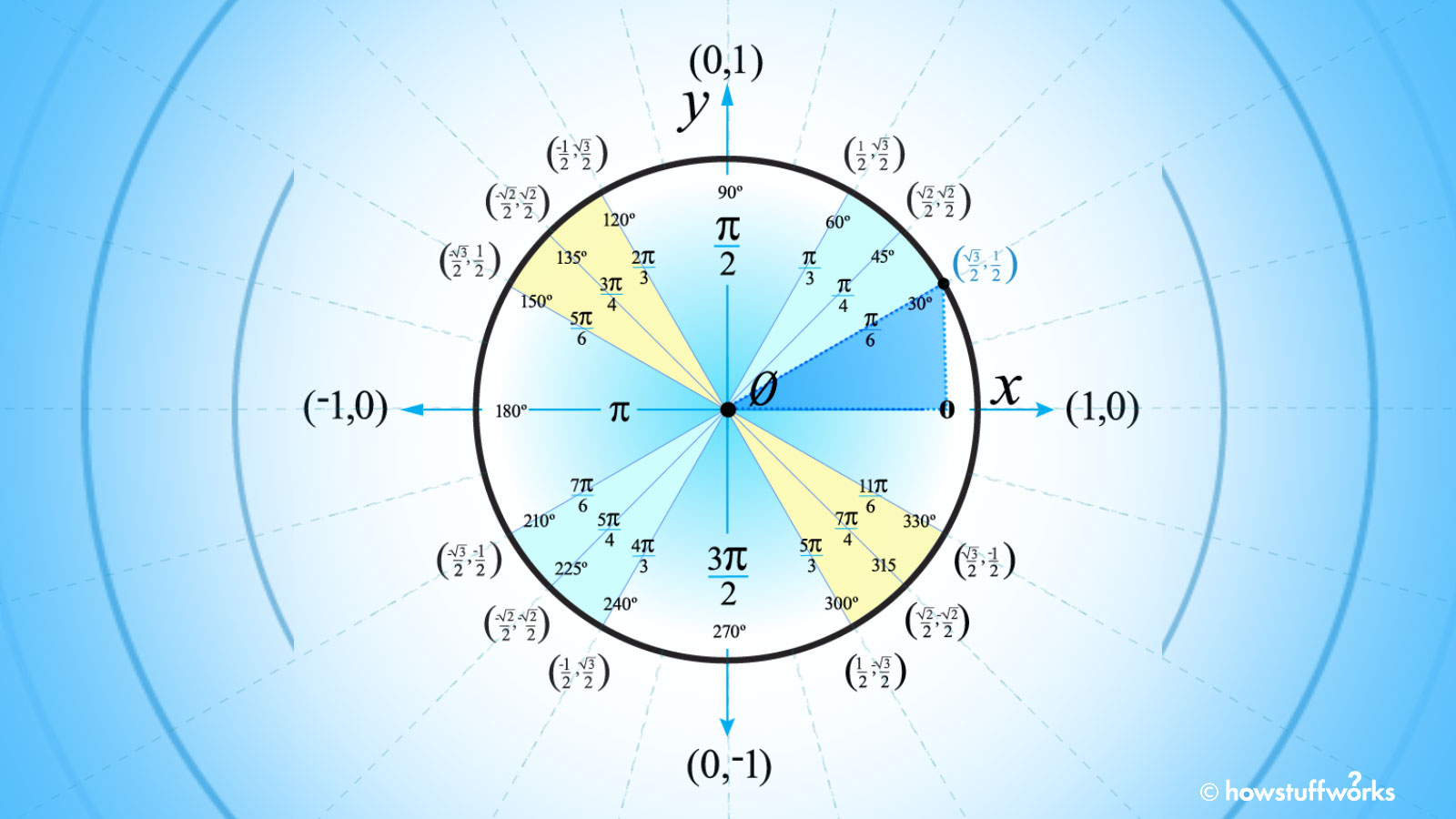



How To Use The Unit Circle In Trig Howstuffworks
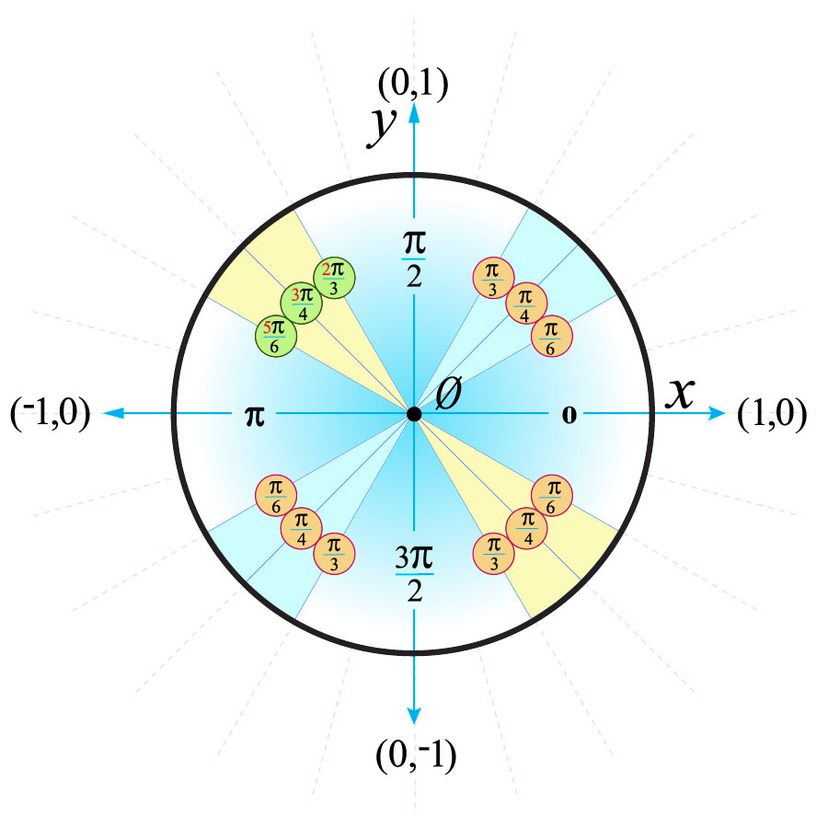



How To Use The Unit Circle In Trig Howstuffworks
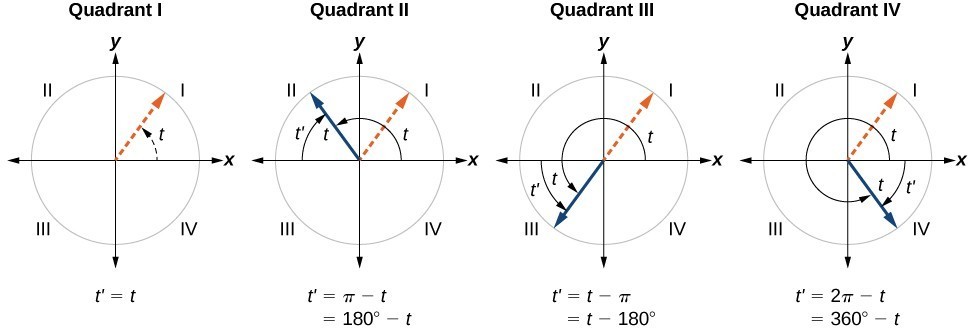



Section 4 4 Reference Angles Precalculus



0 件のコメント:
コメントを投稿